Given a set of time series data that are not necessarily generated by a stationary time series, we can then fit a ARIMA model to the series. That is to say, if the data exhibit no appearent deviations from stationarity and have a rapidly decreasing autocovariance function, we can then fit ARMA model to the mean-corrected data. Otherwise, fit ARIMA model.

• Stationarity

Statistically, a strictly stationary time series means the random variables Xt are identically distributed. That is to say, a stationary time series is one whose statistical properties such as mean, variance, and autocorrelation are all constant over time. A stationary series is relatively easy to predict: you simply predict that its statistical properties will be the same in the future as they have been in the past!
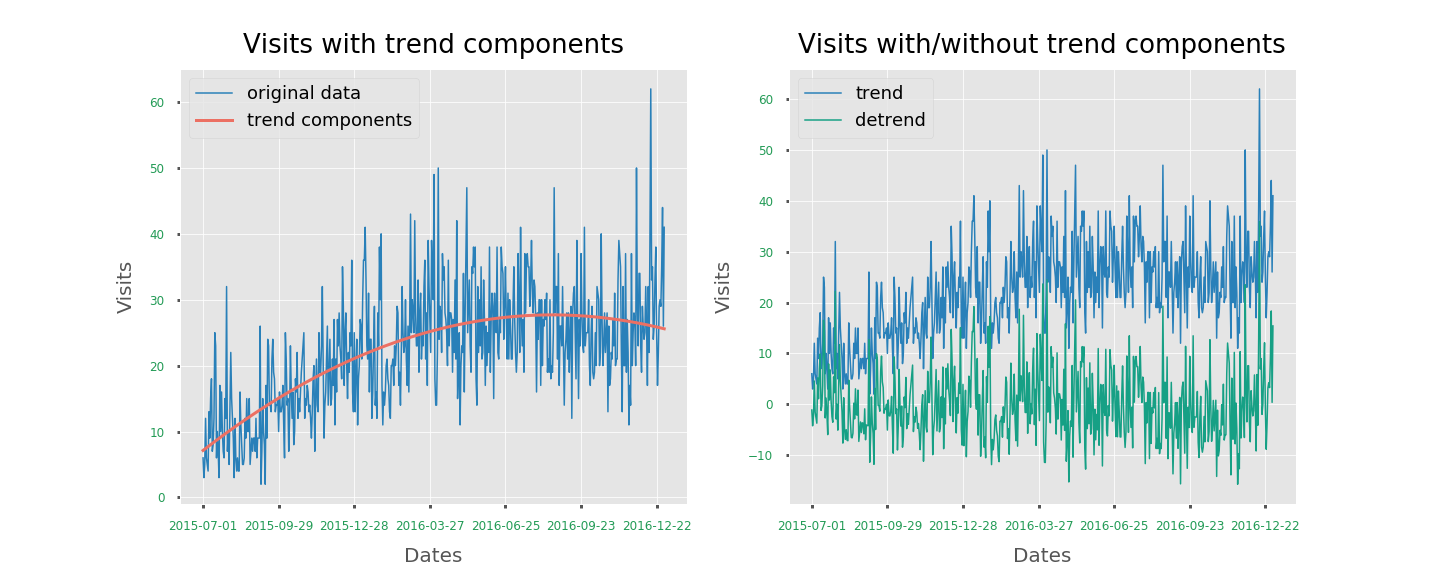
For example, trend and seasonal components are the characteristics suggesting nonstationarity, once we remove the components, the series will become stationary.
We are able to test the staionarity according to the Augmented Dickey-Fullter test, whose null hypothesis is the presence of a unit root in time series, and alternative hypothesis is the stationarity or trend-stationarity of the series.

• ARMA model

A time series Xt is an ARMA(p,q) process if Xt is stationary and if for every t satisfy:

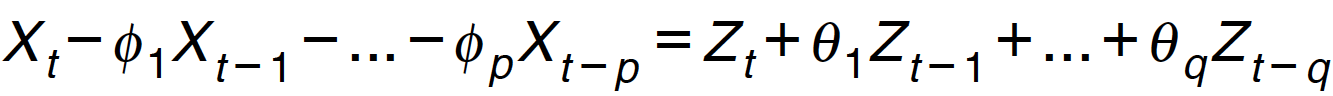
where Zt follows white noise distribution and the polynomials have no common factors.

Statistically, if d is a nonnegative integer, then Xt is an ARIMA(p,d,q) process if 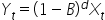is a causal ARMA(p,q) process.
ARIMA is a generalized ARMA. The part "Integrated" means the differencing step, which can eliminate the non-stationarity and fit ARMA model then.

            ● AR - evolving variable of interest is regressed on its prior values
            ● MA - regression error is linear combination of error terms whose values occurred contemporaneously
            ● I - Integratd, data values have been replaced with the difference between their values and the previous values

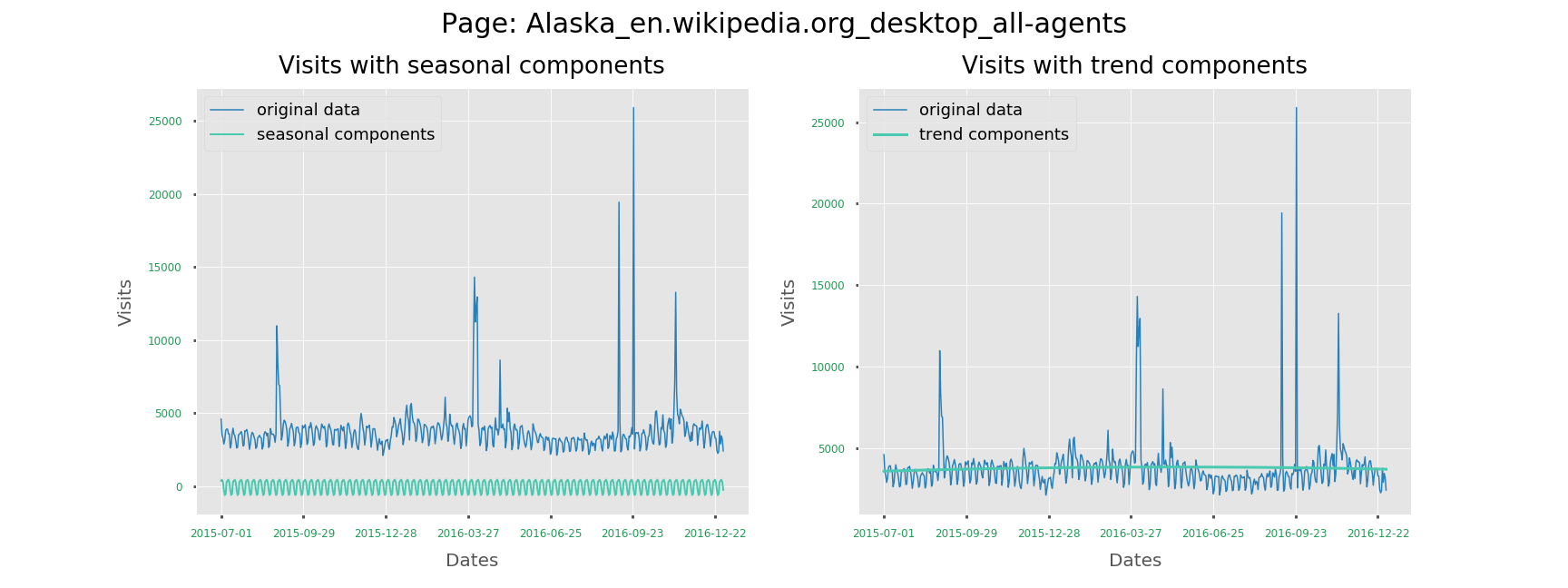
Use Augmented Dickey-Fuller test, and we got 0.000041 as the p-value and conclude that the visits series is stationary, which means we do not have to fit ARIMA model for this series. We only need ARMA instead.

Since the series is stationary, we have tried 0 to 5 for both p parameter (AR part) and q parameter (MA part), then compared their AICC (Akaike Information Criterion corrected) and selected the model with lowest AICC value. AICC is especially developed for small sample size.

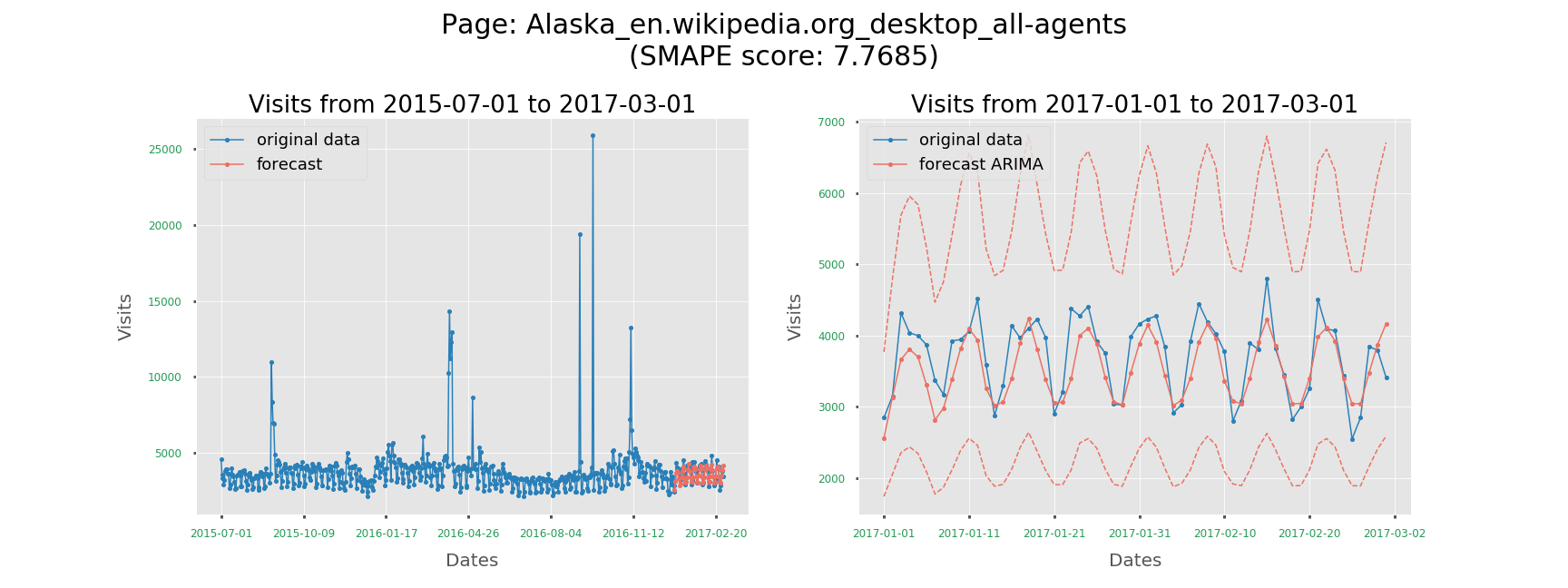
ARIMA (or ARMA) is time consuming. No seriously, it's SUPER SLOW.
The whole process of each series--detrending and deseaonizing the series, train the model and forecasting --takes 1 min. It's not crazy if we only have one series to forecast, but if we have 145k series, we will need:

Ugh, even the competition has only 90 days to finish it.

Compared to ARIMA, fitting ARMA is definitely easier if the series is stationary. Also, if the series has high standard deviation, which means it's autocovariance is high and might differs with time, then the series might be more interesting to forecast.
Therefore, we select the stationary pages based on their augmented Dickey-Fuller test results and the pages with standard deviation larger than 500. After filtering out, we have a subset including 67059 pages.

Although some of the series have warning because of non-stationarity (since augmented Dickey-Fuller test is not 100% robust), but most of them perform pretty well! It results in average 39.6649 for 1867 pages.

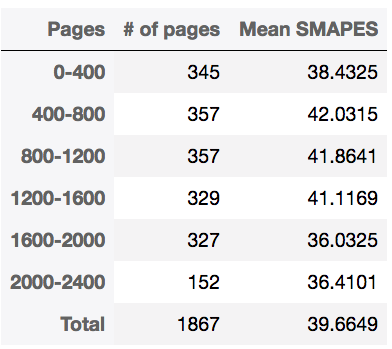
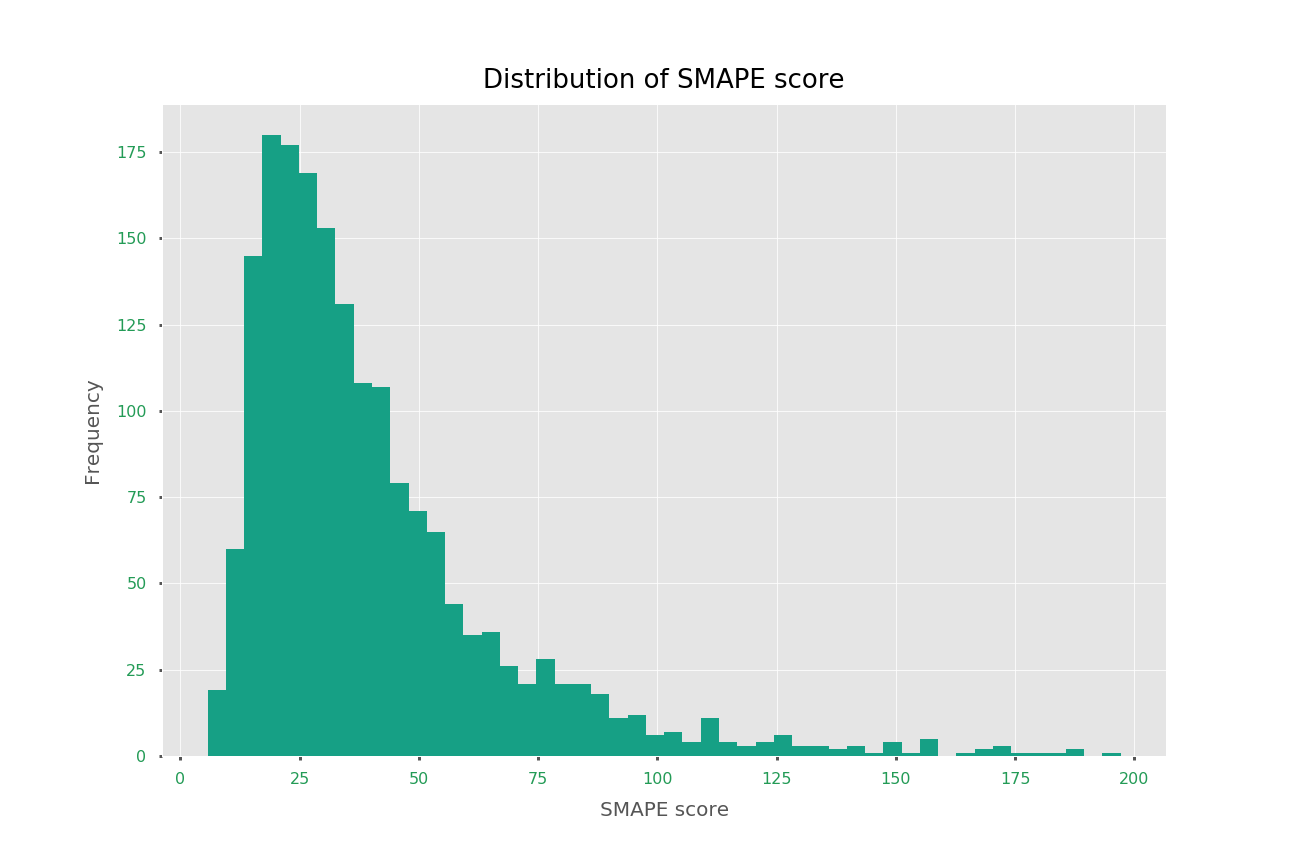
Even though it performs well on those selected series, it's still time consuming. We now have 67059 pages, and it will still take (67059 pages)/(60 mins)/(24 hrs) = 47 days.
No! Never! Never ever! That's why we are not stopping here, we are trying another model and training all the series at once.